Answer:
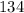 adult tickets and
adult tickets and
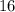 child tickets were sold.
child tickets were sold.
Explanation:
Let
 represents the number of adult tickets sold and
represents the number of adult tickets sold and
 represents the number of child tickets.
represents the number of child tickets.
The total number of tickets sold was
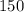 . So we can write the equation,
. So we can write the equation,
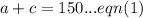
Adult tickets were sold at $
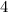 each. This means that,
each. This means that,
 number of adult tickets will yield $
number of adult tickets will yield $
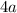 .
.
Child tickets were sold at $
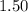 each. This means that,
each. This means that,
 number of adult tickets will yield $
number of adult tickets will yield $
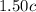 .
.
The total amount collected was $
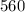 .
.
We can write this equation for the total amount collected.
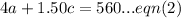
Let us make
 the subject in equation (1) to get,
the subject in equation (1) to get,
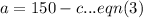
We put equation (3) in to equation (2) to get,
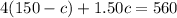
We expand the brackets to get,

We group like terms to get,
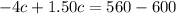
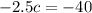
We divide both sides by
 to get,
to get,
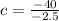
This implies that,

We substitute
 into equation (3) to get,
into equation (3) to get,
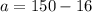
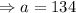
Hence
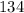 adult tickets and
adult tickets and
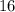 child tickets were sold.
child tickets were sold.