Answer:
[0,600]
Explanation:
We have been given an equation
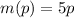 that gives the the amount of money made, in hundreds of dollars, when p apartments are rented.
that gives the the amount of money made, in hundreds of dollars, when p apartments are rented.
Since we know that the range is the resulting y-values we get after substituting all the possible x-values.
Range will be the set of values of m(p) for this function.
Minimum value of p can be 0 as we can not rent negative number of apartments, so minimum value of m(p) will be 0 too.
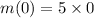
The maximum value of p can be 120 as there are 120 apartments to be rented. Let us find maximum value of m(p) by substituting p=120 in our given equation.
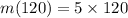

We can see that minimum value of m(p) is 0 and maximum value of m(p) is 600, therefore, range of our given function is [0,600].