Answer:
$285,413.23
Explanation:
We know the annuity formula is given by,
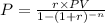 ,
,
where P = regular payment, PV = present value, r = rate of interest and n = time period.
According to the question, we need to find the money to be deposited at the start of the year i.e. PV
So, re-arranging the formula and substituting the values gives us,
![PV=(25312 * [1-(1+0.062)^(-20)])/(0.062)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3ft59rtwi6a1f2j4zbwgn9672j6z10z2id.png)
i.e.
![PV=(25312 * [1-(1.062)^(-20)])/(0.062)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/gp9ek21ytzfd7507w4lwzbkvmdgbubbjkm.png)
i.e.
![PV=(25312 * [1-0.3003])/(0.062)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/bnhto0lvt3an44ab2gtm8fvu0gled5oeaq.png)
i.e.

i.e.
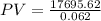
i.e.
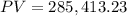
Hence, the amount to be deposited at the start of the year is $285,413.23.