Answer:
Hence, the probability that a teen eats vanilla ice cream, given that he/she eats chocolate ice cream is:
2/5
Explanation:
Let A denote the event that teen eats Vanilla ice-cream.
B denote the event that teen eats Chocolate ice-cream.
and A∩B denote the event that teen eats both chocolate and vanilla ice-cream.
Now , let P be the probability of an event.
We are asked to find:
P(A|B)
We know that the probability i.e. P(A|B) is given by:
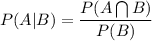
We are given:
Let x be the total number of people who are surveyed.
We have:
A=0.6 x.
B=0.5 x
A∩B=0.2 x
Hence,
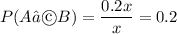
and,
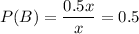
( Since, 0.2+0.3=0.5)
Hence,
P(A|B)=0.2/0.5
i.e.
P(A|B)=2/5