Answer:
Given Inequalities are,

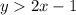
We need to graph the in equality.
First we find the point to draw the lines of the inequality.
By taking them equal we find point.
Consider,
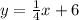
put, x = 0 ⇒ y = 6
put x = 4 ⇒ y = 1 + 6 = 7
So point to draw first line ( 0 , 6 ) and ( 4 , 7 )
Now Consider,
y = 2x - 1
put , x = 0 ⇒ y = -1
put , x = 4 ⇒ y = 8 - 1 = 7
So Points of the second line is ( 0 , -1 ) and ( 4 , 7 )
Since, the inequalities are strict then in graph lines drawn is dotted line as point on line does not includes in the inequality.
For Inequality put ( 0 , 0 )

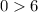
origin does not satisfy it. So, Region we shade is opposite to side in which origin belong.
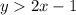

origin does satisfy it. So, Region we shade is to side in which origin belong.
Therefore, The graph we get is attached.