Answer:
(-3, 4/375)
Explanation:
Given : The function
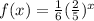 is reflected across the y-axis to create the function g(x).
is reflected across the y-axis to create the function g(x).
To Find: Which ordered pair is on g(x)?
Solution:
Rule of reflection over y axis : (x,y)→(-x,y)
So, when the function
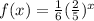 is reflected across the y-axis
is reflected across the y-axis
So, we obtain a function :

So,
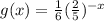
Now substitute the given options to check which satisfies the equation.
a.(-3, 4/375)
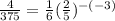

Thus Option A lies on g(x)
b.(-2, 25/24)
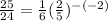
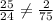
c.(2, 2/75)

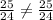
d.(3, -125/48)
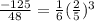
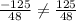
So, option A is true
(-3, 4/375) lies on g(x)