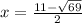Question

Which two values of x are roots of the polynomial below x^2 - 11x + 13

Answer 1

Because 13 is a prime number, we cannot use the AC method to simplify.

We can instead use the quadratic formula.

`(-b +/- √(b^2 - 4ac) )/(2a)`

11 +/- √121 - 52 / 2

11 +/- √69 / 2

11 +/- 8.3 / 2

(11 + 8.3)/2 = 9.65

(11 - 8.3)/2 = 1.35

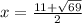The roots of the polynomial are 9.65 and 1.35.

Answer 2

`x=(11+√(69))/(2)` and
`x=(11-√(69))/(2)`

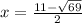
Explanation:

`x^2-11x+13`

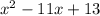
13 is a prime number . we cannot factor it because we cannot find two factors whose product is 13 and sum is -11. Apply quadatic formula to find the x values

Given polynomial is in the form of ax^2+bx+c

a= 1, b= -11 and c=13

`x=(-b+-√(b^2-4ac))/(2a)`

Plug in the values in the formula

`x=(11+-√((-11)^2-4(1)(13)))/(2(1))`

`x=(11+-√(69))/(2(1))`

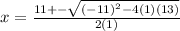
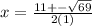
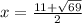`x=(11+√(69))/(2)` and
`x=(11-√(69))/(2)`