Question

Vector u= <9,-2> v=<-1,7> w=<-5,-8> arrange the vector operations in ascending order of their magnitudes of their resultant vectors

Operations:
1.) -1/2u + 5v
2.) 1/6 (u+2v-w)
3.)5/2u-3w
4.)u-3/2v+2w
5.)-4v+1/2w
6.)3u-v-5/2w

Answer 1

Answer: the above answer is correct

Step-by-step explanation: I got this right on Edmentum

Answer 2

The ascending order is:

2) ,4), 5) ,1) ,6) ,3)

Explanation:

We are given u=<9,-2> , v=<-1,7> , w=<-5,-8>

The magnitude of some vector <a,b> is given by:
`√(a^2+b^2)`

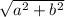
we will find the representation of each of the vectors in order to calculate their magnitudes and arrange them in the ascending order.

1)
`(-1)/(2)u+5v`

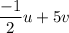
on calculating the value of this operation:

`(-1)/(2)<9,-2>+5<-1,7>=<(-9)/(2),1>+<-5,35>\\  \\=<(-19)/(2),36>`

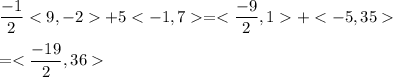
Hence, the magnitude of
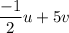`(-1)/(2)u+5v` is:

37.2324

2)
`(1)/(6)(u+2v-w)`

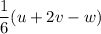
the value of this operation is given as:

`(1)/(6)(<9,-2>+<-2,14>-<-5,-8>)\\ \\=(1)/(6) (<9,-2>+<-2,14>+<5,8>)\\\\=(1)/(6) (<12,20>)\\\\=<2,(10)/(3)>`

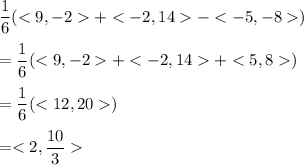
Hence, the magnitude of
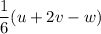`(1)/(6)(u+2v-w)` is:

3.8873

3)
`(5)/(2)u-3w`

The value of this operation is given as:

`(5)/(2)<9,-2>-3<-5,-8>\\\\=<(75)/(2),19>`

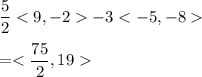
Hence, the magnitude of
`(5)/(2)u-3w` is:

42.0387

4)
`u-(3)/(2)v+2w`

The value of this operation is given as:

`<9,-2>-(3)/(2)<-1,7>+2<-5,-8>\\ \\=<(1)/(2),(-15)/(2)>`

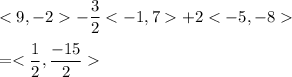
Hence, the magnitude of
`u-(3)/(2)v+2w` is:

7.5166

5)
`-4v+(1)/(2)w`

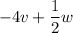
the value of the operation is given as:

`-4<-1,7>+(1)/(2)<-5,-8>\\\\=<(3)/(2),-32>`

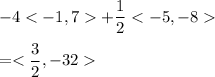
Hence, the magnitude of
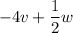`-4v+(1)/(2)w` is:

32.0351

6)
`3u-v-(5)/(2)w`

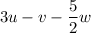
The value of this operation is:

`3<9,-2>-<-1,7>-(5)/(2)<-5,-8>\\ \\=<(81)/(2),7>`

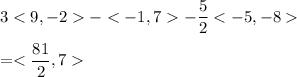
Hence the magnitude of
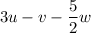`3u-v-(5)/(2)w` is:

40.5863

On Arranging the above operations on the basis of their magnitude in ascending order we get the order as:

2) ,4), 5) ,1) ,6) ,3)