Question

Which expression has an irrational answer?

A) 4+2.5
B) 3x 1/3
C) 2x ^7
D) 1.25+ 4.25

Answer 1

Answer: Option 'B' is correct.

Explanation:

Since we have given that

A) 4+2.5

which is equal to 6.5, which can be written in p\q form:

`(65)/(10)`

So, it is a rational number.

C) 2x^7

It can be written in p\q form:

`(2x^7)/(1)`

D) 1.25+ 4.25

which is equal to 5.50

It can be written in p\q form:

`(55)/(10)`

But,

B)
`3x^(1)/(3)` results irrational numbers as it can't be written in p\q form.

Hence, Option 'B' is correct.

Answer 2

A number is said to be irrational , if the decimal expansion of a number is non terminating non repeating.

For example , 2.01001000100001......., √3,∛5,....

Now coming to Options

(A) 4 + 2.5

4 as well as 2.5 is rational . So sum of two rational is a rational.

(B) 3 ×
`(1)/(3)`

Since 3 is rational , but
`(1)/(3)` is irrational. So product of rational and irrational should be irrational.

Because
`(1)/(3)`= 0.333333.......(non terminating non repeating)

But numerator which is 3 and denominator which is 3 cancels out and result is 1 which is rational number.

(C) 2 × (real number=a )raised to power of 7

=
`2 (a)^7`

=
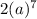
`a^7` has denominator of the form other than
`2^a or 5 ^b or (2 ^a * 5 ^b)` , then it is irrational number.

So,
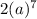`2 (a)^7` is rational or irrational depends on the value of a.

(D) 1.25 + 4.25

Both 1.25 as well as 4.25 are rational. So their sum is rational.

So, option (C)
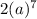`2 (a)^7` may be irrational , it totally depends on the value of a.