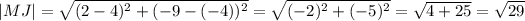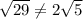No. Because sides JM and KL have different slopes from sides AD and BC .
The formula of a slope:
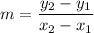
For AD:
We have the points A(2, -2) and D(1, -4). Substitute:
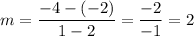
For JM:
We have the points J(4, -4) and M(2, -9). Substitute:
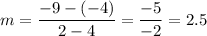
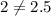
----------------------------------------
Another argument.
No. Because the MJ is not twice as long as AD.
The formula of the length of a segment:
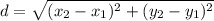
The length of AD:
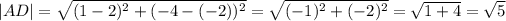
The length of MJ: