Answer:
Option a is correct that is .0156
Explanation:
We have been given the probability of a basketball player scoring is p which is 0.75
So, q is 1-p

Here, we need to find the probability that it will take her more than four shots
We will first find the shots for less than 4 in which we take cases for 1,2 and 3 shots.
We know that total probability is 1.
So, probability of more than four shots + probability of less than 4 shots =1
So, probability of less than 4 shots we will use binomial distribution which is
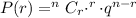
Here,n=3 and r will be 1,2 and 3 we will consider all three cases
We will add all three cases when r=1,2 and 3
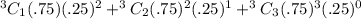
On simplification we will get:0.984375
Probability of three cases that is less than four shots is:=0.984375
So, the required probability is: 1-0.984375=0.015625
Therefore, Option a is correct.