Answer:
No extraneous solution
Explanation:
We have the logarithmic equation given by,
![\log_(2)[\log_(2)(√(4x))]=1](https://img.qammunity.org/2020/formulas/mathematics/high-school/nlm47uk55ymcdeaa98fcbmi51nqfxst10z.png)
i.e.

i.e.

i.e.
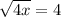
i.e.
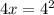
i.e.

i.e.

So, the solution of the given equation is x=4.
Now, as we domain of square root function is x > 0 and also, the domain of logarithmic function is
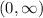 .
.
Therefore, the domain of the given function is x > 0.
We know that the extraneous solution is the solution which does not belong to the domain.
But as x=4 belongs to the domain x > 0.
Thus, x = 4 is not an extraneous solution.
Hence, this equation does not have any extraneous solution.