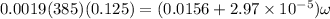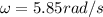Question

A target in a shooting gallery consists of a vertical square wooden board, 0.250 m on a side and with mass 0.750 kg, that pivots on a horizontal axis along its top edge. the board is struck face-on at its center by a bullet with mass 1.90 g that is traveling at 385 m/s and that remains embedded in the board. (a) what is the angular speed of the board just after the bullet's impact?

Answer 1

Here in this case since there is no torque about the hinge axis for the system of bullet and block then we can say that angular momentum of this system will remain conserved

`L_i = L_f`

`mv (L)/(2) = (I_1 + I_2)\omega`

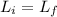
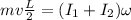
here we will have

L = 0.250 m

v = 385 m/s

m = 1.90 gram

now moment of inertia of the plate will be

`I_1 = (ML^2)/(3)`

`I_1 = (0.750 (0.250)^2)/(3) = 0.0156 kg m^2`

`I_2 = m((L)/(2))^2 = 0.0019(0.125)^2 = 2.97 * 10^(-5) kg m^2`

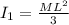
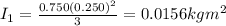
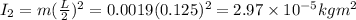
now from above equation

`0.0019 (385)(0.125) = (0.0156 + 2.97 * 10^(-5))\omega`

`\omega = 5.85 rad/s`