Answer:
6032 g
Explanation:
The battery can be modeled as a cylinder.
Volume of a cylinder
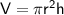
where:
- r is the radius
- h is the height
Given:
Substitute the given values into the formula and solve for v:

Density equation
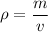
where:
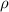 is density
is density- m is mass
- v is volume
Given:
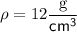
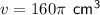
Substitute the given values into the Density equation and solve for m:
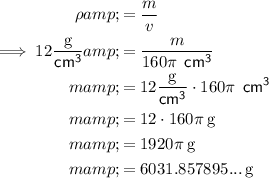
Therefore, the total mass of the battery to the nearest gram is 6032 g.