Question

A scientist running an experiment starts with 100 bacteria cells. These bacteria double their population every 15 hours. Find how long it takes for the bacteria cells to increase to 300. Use the formula , where  is the original number of bacteria cells,  is the number after t hours, and d is the time taken to double the number.

Answer 1

it takes 24 hours for the bacteria cells to increase to 300

Explanation:

WE use the formula

`C= A(b)^{(t)/(d)}`

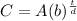
Where A is the initial amount of bacteria= 100

bacteria doubles every 15 hours so b=2

d= 15 because d is the time taken to double the number

t is the number of hours

c is the number of bacteria after t hours = 300

Plug in all the values and solve for 't'

`300= 100(2)^{(t)/(15)}`

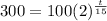
Divide both sides by 100

`3=(2)^{(t)/(15)}`

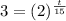
Now we take log on both sides

`log(3)=log(2)^{(t)/(15)}`

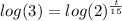
As per log property we can move the exponent before log

log a^m = m log(a)

`log(3)=(t)/(15)log(2)`

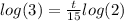
Divide both sides by log(2)

`(log(3))/(log(2)) = (t)/(15)`

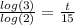
Multiply both sides by 15

`(log(3))/(log(2))*15=t`

t = 23.77

So its approximately 24 hours