Question

I do not understand this question and it will be kind if you help a kid in need

Solve for t, x, or y:

Answer 1

x =
`(mn(q-p))/(n-m)`

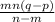
Explanation:

collect the fractional terms on the left side of the equation and other terms on the right side

subtract
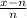`(x-n)/(n)` from both sides

`(x-m)/(m)` -
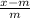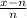`(x-n)/(n)` + p = q

subtract p from both sides

`(x-m)/(m)` -
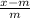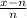`(x-n)/(n)` = q - p

We require the fractions to have a common denominator of mn

multiply the numerator/denominator of the first fraction by n and the numerator/denominator of the second fraction by m

`(n(x-m))/(mn)` -
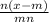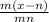`(m(x-n))/(mn)` = q - p

distribute and simplify the numerators of the fractions

`(nx-nm-mx+mn)/(mn)` = q - p

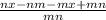`(nx-mx)/(mn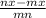)` = q - p

factor out x from each term on the numerator

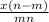`(x(n-m))/(mn)` = q - p

multiply both sides by mn

x(n - m) = mn(q - p)

divide both sides by (n - m)

x =
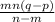`(mn(q-p))/(n-m)` → n ≠ m