The key idea here is that
speed of plane in wind = (speed of plane in air) + (speed of wind)
Let
 be the speed of the plane in still air, and
be the speed of the plane in still air, and
 the wind speed. A tailwind blows in the same direction as the plane, so for the first leg of the trip, we have
the wind speed. A tailwind blows in the same direction as the plane, so for the first leg of the trip, we have

For the return trip, the wind would blow in the opposite direction:
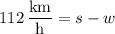
Solve this system and you'll find
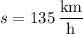 and
and
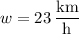 .
.