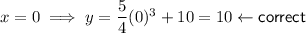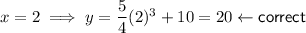Question

asked Dec 17, 2023 213k views

2 Answers

Jianpx · Answer 1 · 2023-12-24T07:22:01+0000

Answer:

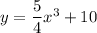
y=(5)/(4)x^3+10

Explanation:

Given information:

Create two equations by substituting the given points into the given equation:

Equation 1: point (0, 10)

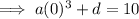
$\implies a(0)^3+d=10$

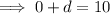
$\implies 0+d=10$

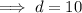
$\implies d=10$

Equation 2: point (2, 20)

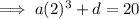
$\implies a(2)^3+d=20$

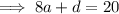
$\implies 8a+d=20$

Substitute Equation 1 into Equation 2 and solve for a:

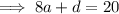
$\implies 8a+d=20$

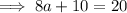
$\implies 8a+10=20$

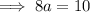
$\implies 8a+10-10=20-10$

$\implies 8a=10$

$\implies (8a)/(8)=(10)/(8)$

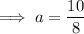
$\implies a=(10)/(8)$

$\implies a=(5)/(4)$

Finally, substitute the found values of a and d into the original formula:

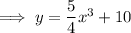
$\implies y=(5)/(4)x^3+10$

Check by substituting the x-values of the two given points into the found equation:

$x=0 \implies y=(5)/(4)(0)^3+10=10 \leftarrow \textsf{correct}$

$x=2 \implies y=(5)/(4)(2)^3+10=20 \leftarrow \textsf{correct}$

Please log in or register to add a comment.