Answer:
Explanation:
According to given equation
A =
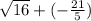 ;
;
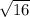 can be simplified to 4.
can be simplified to 4.
Sum :
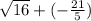 =
=
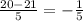
4 is a rational number and
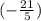 is also a rational number.
is also a rational number.
Sum of two rational number is always a rational number.
Therefore,
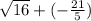 is a rational number.
is a rational number.
B = π+24 ; π is an irrational and 24 is a rational number.
Sum of an irrational and a rational is always a rational number.
Therefore, π+24 is an irrational number.
Sum = π+24
C =
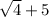 ;
;
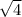 can be simplified to 2.
can be simplified to 2.
2 is a rational number and 5 is also a rational number.
Sum = 2+5=7
Sum of two rational number is always a rational number.
Therefore,
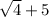 is a rational number.
is a rational number.
D =
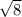 +π ; π is an irrational and
+π ; π is an irrational and
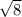 is also an irrational number.
is also an irrational number.
Sum =
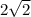 +π
+π
Sum of two irrational number is always an irrational number.
Therefore,
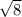 +π is an irrational number.
+π is an irrational number.
E=
![√(36) +\sqrt[3]{27}](https://img.qammunity.org/2020/formulas/mathematics/high-school/j0oghr59sh5bxf4zly5dmor71uxx53vclf.png) ;
;
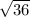 can be simplified to 6 and
can be simplified to 6 and
![\sqrt[3]{27}](https://img.qammunity.org/2020/formulas/mathematics/high-school/2vajawwf8jn7vk72b8sbgveo1dmsmnvdxx.png) can be simplified to 3.
can be simplified to 3.
6 is a rational number and 3 is also a rational number.
Sum = 6+3=9.
Sum of two rational number is always a rational number.
Therefore,
![√(36) +\sqrt[3]{27}](https://img.qammunity.org/2020/formulas/mathematics/high-school/j0oghr59sh5bxf4zly5dmor71uxx53vclf.png) is a rational number.
is a rational number.
F =
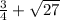 ; \frac{3}{4} is a rational number and \sqrt{27} an irrational number.
; \frac{3}{4} is a rational number and \sqrt{27} an irrational number.
Sum =
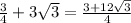
Sum of an irrational and a rational is always a rational number.
Therefore,
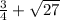 is an irrational number.
is an irrational number.