Answer:
C) y=x^2-2x+6
Explanation:
We are given three points
(1,5) (-1,9) and (4,14)
We can verify each options
option-A:
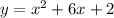
we will verify each points
At (1,5):
we can plug x=1 and check whether y=5
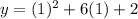
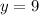
It does not satisfy point
So, this is FALSE
option-B:
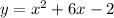
we will verify each points
At (1,5):
we can plug x=1 and check whether y=5
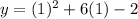
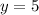
It satisfies point
At (-1,9):
we can plug x=-1 and check whether y=9
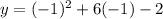
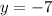
It does not satisfy point
So, this is FALSE
option-C:
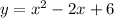
we will verify each points
At (1,5):
we can plug x=1 and check whether y=5

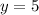
It satisfies point
At (-1,9):
we can plug x=-1 and check whether y=9

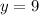
So, it satisfies point
At (4,14):
we can plug x=4 and check whether y=14

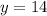
So, it satisfies point
so, this is TRUE