Question

A ball is Thrown into the air with an upward velocity of 24 ft./s it’s height in feet after T seconds is given by the function H equals -16 T squared +24 T +7 in how many seconds does a bowl reach its maximum height what is the balls maximum height

Answer 1

After 0.75 seconds the ball would reach it's maximum height of 16 feet.

Explanation:

We are given a quadratic function
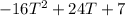`-16T^2+24T+7` for height of the ball after T seconds.

We need to find the time T when ball would reach at it's maximum height and also maximum height of the ball.

In order to find the maximum height of the ball, we need to find the x-coordinate of the vertex.

x-coordinate of the vertex is given by formula

x =
`(-b)/(2a)`.

For the given quadratic a=-16 and b= 24.

Plugging a=-16 and b= 24 in above formula of x-coordinate of the vertex.

`x=(-24)/(2(-16)) = (-24)/(-32) =(3)/(4)= 0.75`.

Now, plugging x=0.75 in given quadratic
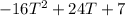`-16T^2+24T+7`, we get

`-16(0.75)^2+24(0.75)+7`

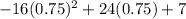
= -16(0.5625)+18+7

= -9+25

=16.

Therefore, after 0.75 seconds the ball would reach it's maximum height of 16 feet.