Question

A bike shop owner rents out bikes and scooters. The cost to rent a bike is $15 plus $8 per hour for each hour the bike is rented. The cost to rent a scooter is $35 plus $5 per hour for each hour the scooter is rented. Which equation has a greater rate of change? The equation that represents the cost of renting a bike or the equation that represents the cost of renting a scooter.

A. The scooter rental has a rate of change of 35, which is greater than the rate of change of the bike rental.

B.The scooter rental has a rate of change of 40, which is greater than the rate of change of the bike rental.

C.The bike rental has a rate of change of 8, which is greater than the rate of change of the scooter rental.

D.The bike rental has a rate of change of 23, which is greater than the rate of change of the scooter rental.

Answer 1

C.The bike rental has a rate of change of 8, which is greater than the rate of change of the scooter rental.

Step-by-step explanation:

Let x be the number of hours.

We have been given that the cost to rent a bike is $15 plus $8 per hour for each hour the bike is rented. We can represent this information in an equation as:

`\text{The cost of renting a bike for x hours}=8x+15`

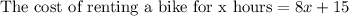
We are also given that the cost to rent a scooter is $35 plus $5 per hour for each hour the scooter is rented. We can represent this information in an equation as:

`\text{The cost of renting scooter for x hours}=5x+35`

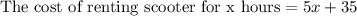
Since we know that the line of an equation in slope-intercept form is:
`y=mx+b`, where,

m = Slope of line or rate of change.

b = The y-intercept.

Upon comparing our equation with the slope-intercept form of equation we can see that the rate of change of the equation that represents the cost of renting a bike is 8, while rate of change of the equation that represents the cost of renting a scooter is 5.

Since 8 is greater than 5, therefore, the equation representing the cost of renting a bike has a greater rate of change and option C is the correct choice.