Question

Sarah would like to make a 6lb nut mixture that is 60% peanuts and 40% almonds. She has several pounds of a mixture that is 80% peanuts and 20% almonds and several pounds of a mixture that is 50% peanuts and 50% almonds.

a) What is the system that models this situation?


b) What is the solution to the system? How many pounds of the 80/20 mixture? How many pounds of 50/50 mixture? SHOW YOUR WORK!

Answer 1

Answer:
`\left \{ {{A+B\ =\ 6}\atop{0.8A+0.5B\ =\ 0.6(6)}} \right.`

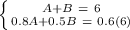
2 lbs of 80/20 and 4 lbs of 50/50 mixtures

Explanation:

Let A represent the quantity of the 80/20 mixture. Let B represent the quantity of the 50/50 mixture.

Let's solve based on peanuts:

• A has 80% peanuts = 0.8
• B has 50% peanuts = 0.5
• Mixture has 60% peanuts = 0.6

First, set up the equations:

• Quantity: A + B = 6
• Peanut % x Quantity: 0.8A + 0.5B = 0.6(6)

Now, solve the system above using substitution: A + B = 6 ⇒ B = 6 - A

0.8A + 0.5(6 - A) = 0.6(6)

0.8A + 3 - 0.5A = 3.6

3 + 0.3A = 3.6

0.3A = 0.6

A = 2

Lastly, plug in A (above) into the Quantity equation to solve for B:

A + B = 6

(2) + B = 6

B = 4

SIDE NOTE: You could have solved based on almonds by setting up the system as:

• Quantity: A + B = 6
• Almond % x Quantity: 0.2A + 0.5B = 0.4(6)

which would give the same answer (A = 2, B = 4)