Question

For the triangle shown below, find the circumcenter and orthocenter

Answer 1

Answer: Circumcenter =
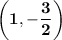`\bold{\bigg(1,-(3)/(2)\bigg)}` Orthocenter = (-4, -6)

Step-by-step explanation for Circumcenter:

Step 1: Find the midpoint of a line: I chose (-4, 3) and (-4, -6)

`\bigg((-4-4)/(2),(3-6)/(2)\bigg)=\bigg((-8)/(2),(-3)/(2)\bigg) = \bigg(-4,-(3)/(2)\bigg)`

Step 2: Find the perpendicular line that passes through that point:

Since it is a vertical line, the perpendicular line is
`y=-(3)/(2)`

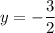
Step 3: repeat Steps 1 and 2 for another line: chose (-4, -6) and (6, -6)

`\bigg((-4+6)/(2),(-6-6)/(2)\bigg)=\bigg((2)/(2),(-12)/(2)\bigg) = (1,-6)`

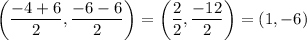
Since it is a horizontal line, the perpendicular line is: x = 1

Step 4: Find the intersection of the two lines
`\bigg(y=-(3)/(2)\ \text{and}\ x = 1\bigg)`

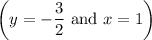
Their point of intersection is:
`\bigg(1, -(3)/(2)\bigg)`

*************************************************************************************

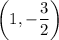
Step-by-step explanation for Orthocenter:

Step 1: Find the perpendicular slope of a line: I chose (-4, 3) and (-4, -6)

Slope is undefined. Perpendicular slope is 0.

Step 2: Use the Point-Slope formula to find the equation of the line that passes through the vertex that is opposite of the line from Step 1 and has the perpendicular slope (found in Step 1).

Vertex (6, -6) and m⊥ = 0 ⇒ y + 6 = 0(x - 6) ⇒ y = -6

Step 3: repeat Steps 1 and 2 for another line: chose (-4, -6) and (6, -6)

Slope is 0. Perpendicular slope is undefined (x = __ )

Vertex (-4, 3) and m⊥ = undefined ⇒ x = -4

Step 4: Find the intersection of the two lines
`(y=-6\ \text{and}\ x = -4)`

Their point of intersection is: (-4, -6)