1 Answer

CamilB · Answer 1 · 2020-02-17T14:34:57+0000

Answer:

Given : PQR is a triangle.

Such that,
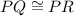
$PQ \cong PR$

Prove:
$\angle Q \cong \angle R$

Construct median PM.

⇒M is the mid point of line segment QR ( by the definition of median )

Therefore,
$QM\cong MR$ (By the definition of mid point)

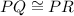$PQ\cong PR$ (given)

$PM \cong PM$ ( reflexive)

Thus, By SSS congruence postulate,

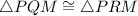
$\triangle PQM \cong \triangle PRM$

Thus, BY CPCTC,

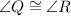
$\angle Q\cong \angle R$

Hence proved.

Please log in or register to add a comment.