Answer:
Yes, the triangle is a right triangle.
Step-by-step explanation:
Since we know that slope formula of the line connecting two points is:
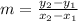 , where,
, where,
m = Slope of the line.
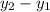 = Difference between y-coordinates of two points.
= Difference between y-coordinates of two points.
 = Difference between corresponding x-coordinates of same two points.
= Difference between corresponding x-coordinates of same two points.
Let us find slope of the line connecting points J(1,1) and K(2,4).
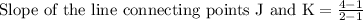
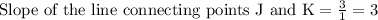
Let us find slope of the line connecting points K(2,4) and L(5,3).
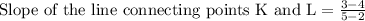
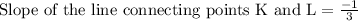
Let us find slope of the line connecting points L(5,3) and J(1,1).
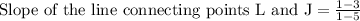
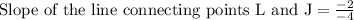
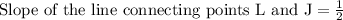
Since we know that perpendicular lines intersect at right angles to one another and the slopes of perpendicular lines are opposite reciprocals of each other.
We can see that slope of line connecting points J and K is 3, while slope of the line connecting points K and L is
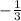 .
.
Since
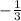 is negative reciprocal of 3, therefore, the triangle is a right triangle.
is negative reciprocal of 3, therefore, the triangle is a right triangle.