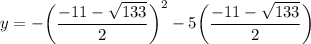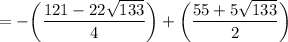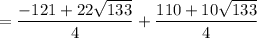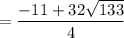Answer:
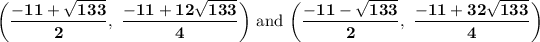
Explanation:
y = -x² - 5x
-6x + y = -3
Use substitution method:
-6x + (-x² - 5x) = -3 substituted "y" with "-x² - 5x"
-x² -11x = -3 simplified left side (added like terms)
-x² - 11x + 3 = 0 added 3 to both sides
Solve using quadratic formula:
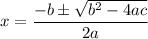
a = -1, b = -11, c = 3
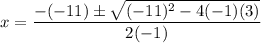
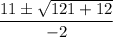
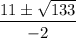
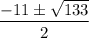
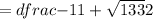 and
and
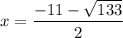
Next, solve for "y" by plugging the x-values above into the equation: y = -x² - 5x
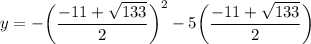
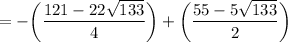
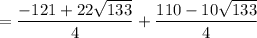
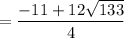
and