Question

Given: ΔACM, m∠C = 90º

CP
⊥
AM
, AC = 15
AP = 9, PM = 16
Find: CP, CM

Answer 1

CM=20 and CP=12

Explanation:

The given triangle ΔACM has the measurements as follows:

m∠C=90°, CP⊥AM, AC=15, AP=9, PM=16.

To Find: CP and CM

We can use Pythagoras theorem to calculate the sides CP and CM.

Pythagoras theorem gives a relation between hypotenuse, base and height/perpendicular of a right angled triangle which is as follows:

`h^(2)=p^(2)+b^(2)`

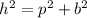
where h is hypotenuse of triangle, b is base and p is perpendicular of triangle.

The figure shows that in ΔACM is a right angled triangle at C where,

AM --> hypotenuse

CM --> base

AC --> height

So substituting values into formula:

`AM^(2)=AC^(2)+CM^(2)`

`25^(2)=15^(2)+CM^(2)`

`625-225=CM^(2)`

`400=CM^(2)`

`√(400) =CM`

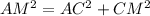
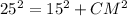
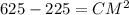
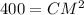
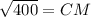
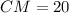`CM=20`, which is required answer.

Similarly, we can see that triangle ΔCPM is also a right angled triangle at P and thus Pythagoras theorem can again be applied to calculate CP. Since CM is the side opposite to right angle P, it is the hypotenuse.

So we have,

`CM^(2)=PM^(2)+CP^(2)`

`20^(2)=16^(2)+CP^(2)`

`400-256=CP^(2)`

`144=CP^(2)`

`√(144) =CP`

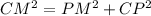
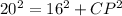
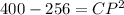
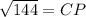
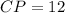`CP=12`, which is required answer.