Question

Solve for x, 0 ≤ x ≤ 360.

1/sin^2 x = 4

A. 30

B. 150

C. 210

D. 330

You can choose more than one !

Answer 1

Hello there,

Solve for x, 0 ≤ x ≤ 360.

1/sin^2 x = 4

Answers: 30 and 150

Answer 2

A & B

Explanation:

`(1)/(sin^2x)=4` can be solved by inverting the fraction and taking the square root.

`(1)/(sin^2x)=4\\\\sin^2x=(1)/(4)\\√(sin^2x)=\sqrt{(1)/(4) }  \\ sin x=(1)/(2)`

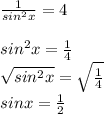
We need an x value that gives 1/2 as its sine value. This means we're referring to a triangle with side measures 1,
`√(3)` and 2. This special triangle has angles 30, 60, and 90. 1/2 matches to a 30 degree angle. All of the options are variations on 30 degrees but not all give the same value.

Sin 30 = 1/2

Sin 150 = 1/2

Sin 210 =-- 1/2

Sin 330 =- 1/2