Question

An airplane is flying at a velocity of 321.71 m/s in a direction 32 degrees north of west. What are the magnitudes and directions of the components of this velocity vector? (2 points)

301.1 m/s to the west, 96.38 m/s to the south
272.8 m/s to the west, 170.5 m/s to the north
102.5 m/s to the west, 264.4 m/s to the north
201.7 m/s to the east, 98.1 m/s to the north

Answer 1

In triangle ABC

AB = V = velocity of the airplane = 321.71 m/s

BC =
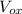`V_(ox)` = horizontal component of the velocity of airplane

AC =
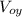`V_(oy)` = vertical component of the velocity of airplane

using the trigonometric formula

Cos32 = BC/AB

Cos32 =
`V_(ox)` /321.71

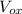`V_(ox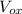)` = (321.71) Cos32

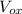`V_(ox)` = 272.83 m/s

direction : towards west

using the trigonometric formula

Sin32 = AC/AB

Sin32 =
`V_(oy)` /321.71

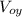`V_(ox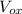)` = (321.71) Sin32

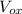`V_(ox)` = 170.5 m/s

direction : towards north

272.8 m/s to the west, 170.5 m/s to the north