The speed of the ball when it returns to the same horizontal level is 8.0 m/s
To find the speed of the ball when it returns to the same horizontal level, we can use the principle of conservation of energy.
The horizontal component of the initial velocity remains constant as there is no horizontal acceleration (neglecting air resistance).
The vertical component of the velocity changes due to gravity.
The horizontal component
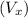 remains the same:
remains the same:
![\[ V_x = V_0 \cos(\theta) \]](https://img.qammunity.org/2020/formulas/physics/middle-school/vge4qhgxpq5tx4ue755neqrbv0x1yyat38.png)
where:
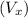 is the horizontal component,
is the horizontal component,
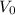 is the initial speed (8.0 m/s),
is the initial speed (8.0 m/s),
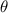 is the angle (35°).
is the angle (35°).
![\[ V_x = 8.0 \, \text{m/s} \cdot \cos(35°) \]\\ V_x \approx 6.58 \, \text{m/s} \]](https://img.qammunity.org/2020/formulas/physics/middle-school/300d9qsilkcmconxgoexyfarlp2wn0xdhr.png)
Now, to find the final speed, we consider the vertical motion.
The vertical component
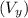 when the ball returns to the same horizontal level is the opposite of the initial vertical component:
when the ball returns to the same horizontal level is the opposite of the initial vertical component:
![\[ V_y = -V_0 \sin(\theta) \]\\V_y = -8.0 \, \text{m/s} \cdot \sin(35°) \]\\V_y \approx -4.58 \, \text{m/s} \]](https://img.qammunity.org/2020/formulas/physics/middle-school/8t292th7vkge12h13xs7qa824v5srfwlf3.png)
Now, use these components to find the total speed (V) using the Pythagorean theorem:
![\[ V = √(V_x^2 + V_y^2) \]\\ V = \sqrt{(6.58 \, \text{m/s})^2 + (-4.58 \, \text{m/s})^2} \]\\ V \approx 7.88 \, \text{m/s} \]](https://img.qammunity.org/2020/formulas/physics/middle-school/eng3fmw8kvn3e164eqciex85aftgq9nevm.png)
Therefore, the speed of the ball when it returns to the same horizontal level is approximately 7.88 m/s. Among the given options, the closest one is: B) 8.0 m/s.
The probable question may be:
1) A ball is thrown at an original speed of 8.0 m/s at an angle of 35° above the horizontal. If there is no air resistance, what is the speed of the ball when it returns to the same horizontal level?
A) 4.0 m/s
B) 8.0 m/s
C) 16 m/s
D) 9.8 m/s