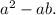Answer:
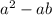
Explanation:
We need to find the sum of
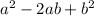 and
and
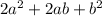 first.
first.
Adding
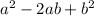 +
+
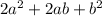
Combining like terms, we get
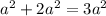
-2ab+2ab = 0
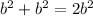
Therefore,
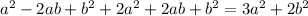 .
.
Now, we need to find the sum of
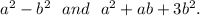 .
.
Adding
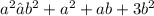 .
.
Combining like terms, we get
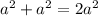
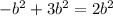 .
.
Therefore,
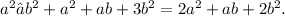
Now, subtracting
 .
.
Distributing minus sign over second parenthesis, we get
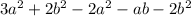 .
.
Combining like terms,
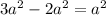

Therefore,
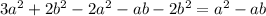 .
.
Therefore, the difference of the sum of
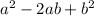 +
+
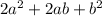 and
and
 is
is