Question

PLEASE HELP!!!!!

If you are given the 3 vertices of a parallelogram below, find the exact coordinates of the 4th vertex. Please find the coordinates for point D:

A (-2, -1)

B (2, 1)

C (0, -3)

D (x, y)

Please explain all the steps and show all work!

Answer 1

Answer: (-4,-5)

Explanation:

Here ABCD is a parallelogram,

Where A≡(-2,-1), B≡(2,1), C≡(0,-3) and D≡(x,y)

By the property of parallelogram,

AB║CD, AD║BC, AB = CD and AD=BC

If AB ║ CD

⇒ Slope of AB = Slope of CD

⇒
`(1-(-1))/(2-(-2)) = (-3-y)/(0-x)`

⇒
`(1+1)/(2+2)) = (-3-y)/(-x)`

⇒
`(2)/(4) = (3+y)/(x)`

⇒
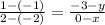
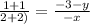
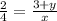
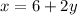`x=6+2y` ------ (1)

Now, AB = CD

`√((2-(-2))^2+(1-(-1))^2) = √((0-x)^2+(-3-y)^2)`

`√(4^2+2^2) = √(x^2+9+6y+y^2)`

`√(16+4) = √(x^2+9+6y+y^2)`

`√(20) = √(x^2+9+6y+y^2)`

`20 = x^2+9+6y+y^2`

`x^2+6y+y^2=11`

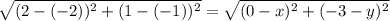
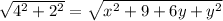
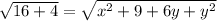
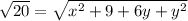
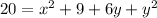
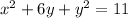
From equation (1)

`(6+2y)^2+6y+y^2=11`

`36+4y^2+24y+6y+y^2=11`

`5y^2+30y+25=0`

`y^2+6y+5=0`

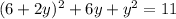
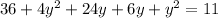
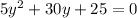
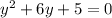
⇒ y = -1 or -5

Again by equation (1)

for y = -1, x = 4

For y = -5, x = -4

Thus the coordinate of D are (4,-1) or ( -4,-5)

But for D≡(4,-1), AD∦BC

While For D≡(-4,-5) AD ║ BC

Thus the coordinates of D are ( -4,-5)