Answer:
Option A is correct.

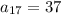
Explanation:
An arithmetic sequence is a sequence of number that the common difference between between the consecutive term is constant.
Explicit formula for arithmetic sequence is given by;
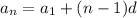
where
n is the number of terms.
 is the first term
is the first term
d is the common difference.
Given the sequence :
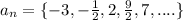
This is an arithmetic sequence with common difference: d =
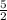
Here,
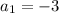
Since;
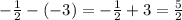
 and so on...
and so on...
Then;
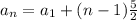
or
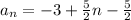
Simplify:
 .....[1]
.....[1]
To find
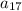 ;
;
put n =17 in [1] we get;
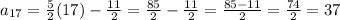
Therefore, the explicit formula for the given sequence is,
 and value of
and value of
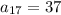 ;
;