Question

How do you solve this: In ?PQR, PQ = 39 cm and PN is an altitude. Find PR if QN = 36 cm and RN = 8 cm.

Answer 1

PR = 17 cm

Explanation:

Given :

In ΔPQR,

PQ = 39 cm

PN is an altitude.

QN = 36 cm

RN = 8 cm.

To Find : Length of PR

Solution :

Since we are given that PN is an altitude .

So, PN divides ΔPQR in two right angled triangles named as ΔPQN and ΔPRN. (Refer attached file)

So, first we find Length of PN in ΔPQN using Pythagoras theorem i.e.

`(Hypotenuse)^(2)=(Perpendicular)^(2) +(Base)^(2)`

`(PQ)^(2)=(PN)^(2) +(QN)^(2)`

`(39)^(2)=(PN)^(2) +(36)^(2)`

`1521=(PN)^(2) +1296`

`1521 -1296=(PN)^(2)`

`225=(PN)^(2)`

`√(225) = PN`

`15 = PN`

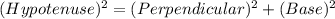
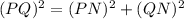
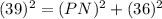
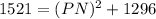
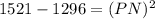
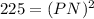
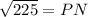
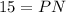
Thus, Length of PN = 15cm

Now to find length of PR we will use Pythagoras theorem in ΔPRN.

`(PR)^(2)=(PN)^(2) +(NR)^(2)`

`(PR)^(2)=(15)^(2) +(8)^(2)`

`(PR)^(2)=225 +64`

`(PR)^(2)=289`

`PR= √(289)`

`PR= 17`

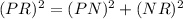
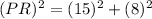
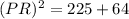
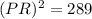
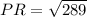
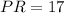
Hence the length of PR = 17 cm