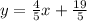Answer:
a)
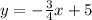
b)
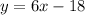
c)
Explanation:
a) The slope / gradient is the coefficient of
 , so for a) it will be
, so for a) it will be
 .
.
C is the y-intercept, so the full equation will be
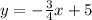 .
.
b) Again, since the slope is 6, we know the coefficient of
 will be 6.
will be 6.
Now, we have a point on the line and so far, we know the equation is
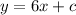 . The coordinates of the point are (2,-6). So now we substitute the y and x values into the equation in order to find C.
. The coordinates of the point are (2,-6). So now we substitute the y and x values into the equation in order to find C.
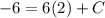
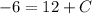
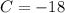
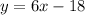
c) To find the gradient we must use the formula
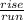 .
.
rise = change in y value
run = change in x value
so, the gradient
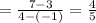
Now the equation is
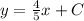
Again, to find C we substitute any of the coordinates into the equation. I will use (-1,3).
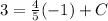
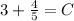

so c) is