Question

Allison is rolling her hula hoop on the playground. The radius of her hula hoop is 35 cm. What is the distance the hula hoop rolls in 4 full rotations? Round your answer to the nearest cm.

Answer 1

the guy above me is correct it is 880cm

Explanation:

on khan academy

Answer 2

Distance covered by hula hoop rolls in 4 full rotations is 880 cm .

Explanation:

Formula

`Perimeter\ of\ a\ circle = 2\pi r`

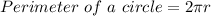
Where r is the radius of the circle.

As given

Allison is rolling her hula hoop on the playground.

The radius of her hula hoop is 35 cm.

r = 35 cm

`\pi = (22)/(7)`

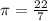
Putting the value in the formula

`Perimeter\ of\ a\ hula hoop = 2* (22)/(7) * 35`

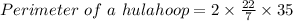
= 220 cm

As given

The hula hoop rolls in 4 full rotations.

Distance covered by hula hoop rolls in 4 full rotations = 220 × 4

= 880 cm

Therefore the Distance covered by hula hoop rolls in 4 full rotations is 880 cm .