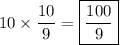Question

How do I solve an endless amount of numbers with a common ratio

..........

etc. 10+1+0.1+0.01+0.001....

Answer 1

Notice that the given sum is equivalent to

`10 + 1 + \frac1{10} + \frac1{10^2} + \frac1{10^3} + \cdots \\\\ ~~~~~~~~~~~~ = 10 \left(1 + \frac1{10} + \frac1{10^2} + \frac1{10^3} + \frac1{10^4} + \cdots\right)`

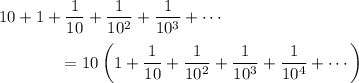
or 10 times the infinite geometric series with ratio 1/10.

To compute the infinite sum, consider the
`n`-th partial sum

`S_n = 1 + \frac1{10} + \frac1{10^2} + \cdots + \frac1{10^(n-1)}`

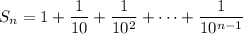
Multiply both sides by the ratio.

`\frac1{10} S_n = \frac1{10} + \frac1{10^2} + \frac1{10^3} + \cdots + \frac1{10^n}`

Subtract this from
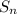`S_n` to eliminate all but the outermost terms,

`S_n - \frac1{10} S_n = 1 - \frac1{10^n} \implies S_n = \frac{10}9 \left(1 - \frac1{10^n}\right)`

As
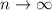`n\to\infty`, the exponential term will decay to 0, leaving us with

`1 + \frac1{10} + \frac1{10^2} + \cdots = \frac{10}9`

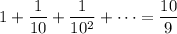
Then the value of the sum we want is

`10*\frac{10}9 = \boxed{\frac{100}9}`

Answer 2

11 .21 add the number together