Question

In △ABC, M∈ AC and N∈ BC . Prove that MN ∥ AB , if: AM/CM =BN/CN

Answer 1

See proof below

Explanation:

1. Consider in triangles ABC and MNC the ratio
`(AC)/(MC).`

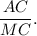
Since
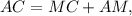`AC=MC+AM,` then

`(AC)/(MC)=(MC+AM)/(MC)=1+(AM)/(MC).`

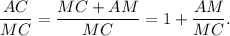
2. Consider in triangles ABC and MNC the ratio
`(BC)/(NC).`

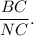
Since
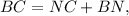`BC=NC+BN,` then

`(BC)/(NC)=(NC+BN)/(NC)=1+(BN)/(NC).`

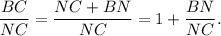
3. You are given that

`(AM)/(MC)=(BN)/(NC),`

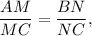
then

`1+(AM)/(MC)=1+(BN)/(NC)\Rightarrow (AC)/(MC)=(BC)/(NC).`

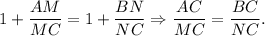
4. The previous statement gives you that triangles ABC and MNC are similar (they have two pairs of proportional sides and common angle C). Similar triangle have congruent corresponding angles. Hence,

• ∠CAB≅∠CMN;
• ∠CBA≅∠CNM.

First pair of angles form corresponding angles at lines MN and AB and transversal BC and second pair of angles form corresponding angles at lines MN and AB and transversal AC. Since corresponding angles are congruent, the lines AB and MN are parallel.