Answer:
The area of rectangle is increased by 200%
Explanation:
Given the ratio of the width to the length of a rectangle is 2:3, respectively.
∴ Width = 2x units
and Length = 3x units
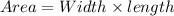
=
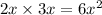 square units
square units
now, if the width of the rectangle is increased by 50% and the length is increased by the same number of units
then width and length becomes
New width=2x+0.05(2x)=2x+x=3x units
and length=3x+3x=6x units
Therefore,
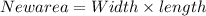
=
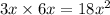 square units
square units
Area increased by percentage =

=

= 200%