The point-slope form:

m - slope
(x₁, y₁) - point
The formula of a slope:
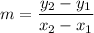
We have the points (3, 95) and (11, 12). Substitute:
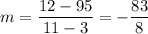
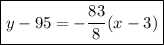 point-slope form
point-slope form
Convert to the slope-ntercept form (y = mx + b)
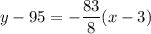 use the distributivie property
use the distributivie property
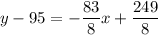 add 95 to both sides
add 95 to both sides
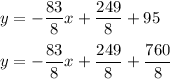
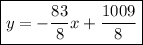 slope-intercept form
slope-intercept form
Convert to the standrd form (Ax + By = C)
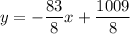 multiply both sides by 8
multiply both sides by 8
 add 83x to both sides
add 83x to both sides
 standard form
standard form