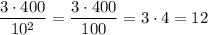Question

Can someone help with this question?

Answer 1

You solve an expression for a variable if that variable sits alone on one side of the equation, and everything else is on the other side.

So, our goal is to leave
`h` alone on the right hand side, and move everything else to the left.

So, we start with

`V = (1)/(3)s^2h`

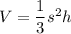
We multiply both sides by 3:

`3V = s^2h`

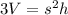
We divide both sides by
`s^2`

`(3V)/(s^2) = h`

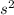
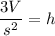
To compute the required height, simply plug in the values:

`(3\cdot 400)/(10^2) = (3\cdot 400)/(100) = 3\cdot 4 = 12`

Answer 2

Answer:
`\bold{h=(3V)/(s^2), \qquad h=12}`

Explanation:

Isolate the variable "h" by multiplying both sides by 3 and dividing both sides by s².

`V=(1)/(3)s^2h`

`(3)V=(3)(1)/(3)s^2h\ \quad \rightarrow\ \quad 3V=s^2h`

`(3V)/(s^2)=(s^2h)/(s^2)\ \quad \rightarrow \quad (3V)/(s^2)=h`

Next, substitute V = 400 and s = 10 to solve for h:

`h=(3(400))/((10)^2)`

`=(1200)/(100)`

`= 12`