Answer:
A) Quantity x minus 5 over quantity x plus 1, where x≠-1 and x≠-9
Explanation:
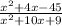
Simplifying the numerator first:
x² + 4x - 45 using the quadratic formula you get;
(x - 5)(x + 9)
Then simplifying the denominator x² + 10x + 9 using a quadratic formula you get;
(x + 1)(x + 9)
Dividing the numerator and denominator now gives;
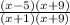
Cancelling (x + 9) throughout leaves you with;
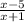
The only restrictions here is if x = 1 and 9 which will give an undefined answer.