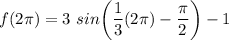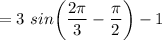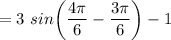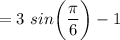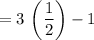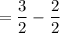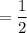Question

A sine function had an amplitude of 3, period of 6pi, horizontal shift of 3pi/2, & vertical shift of -1.

What is the y-value of the positive function when x=2pi?

Answer 1

Answer:
`\bold{y=(1)/(2)}`

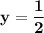
Explanation:

f(x) = A sin (Bx - C) + D

• amplitude = |A|
• period =
  `(2\pi)/(B)`
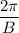
• phase shift =
  `(C)/(B)`
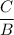
• vertical shift = D

A

amplitude of 3 is given so 3 = |A| → A = ± 3, since it is stated that this is a positive function, then A = 3

B

period of 6π is given so
`6\pi=(2\pi)/(B)\quad \rightarrow \quad B=(2\pi)/(6\pi)\quad \rightarrow \quad B=(1)/(3)`

C

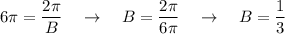
`\text{phase shift is given as}\ (3\pi)/(2)\ \text{so}\ (3\pi)/(2)=(C)/((1)/(3))\quad \rightarrow\quad (((1)/(3))3\pi)/(2)=C\quad \rightarrow\quad (\pi)/(2)=C`

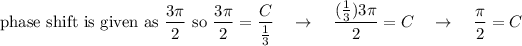
D

vertical shift of -1 is given so -1 = D

Now, substitute the values of A, B, C, and D into the formula (above):

`f(x) = 3\ sin \bigg((1)/(3)x - (\pi)/(2)\bigg) - 1`

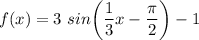
Next, solve when x = 2π

`f(2\pi) = 3\ sin \bigg((1)/(3)(2\pi) - (\pi)/(2)\bigg) - 1`

`= 3\ sin \bigg((2\pi)/(3) - (\pi)/(2)\bigg) - 1`

`= 3\ sin \bigg((4\pi)/(6) - (3\pi)/(6)\bigg) - 1`

`= 3\ sin \bigg((\pi)/(6)\bigg) - 1`

`= 3\ \bigg((1)/(2)\bigg) - 1`

`=(3)/(2)-(2)/(2)`

`=(1)/(2)`