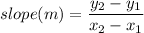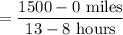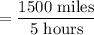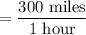Question

I need help with these problems 50 points!!!

Answer 1

Explanation:

1. the rockets rate of change in miles per second is:

(5 - 1)/(2.5*60 - 30) = 1/30 miler per second or 0.033

the rockets rate of change in miles per minute is:

(5 - 1)/(2.5 - 30/60) = 2 miles per minute

2. About $12.50 OR an average of $11.81 over all 9 weeks

3. 300 miles per hour or 5 miles per minute

Answer 2

8. Answer: 0.033 miles per second

Explanation:

Determine the coordinates in like units where x is seconds and y is miles, use the slope formula to find the rate of change, then reduce so the denominator is equal to 1.

(30 seconds, 1 mile) and (2.5 minutes, 5 miles)

= (30 seconds, 1 mile) and (150 seconds, 5 miles)

`slope (m) = (y_2-y_1)/(x_2-x_1)`

`= \frac{5-1\ \text{miles}}{150-30\ \text{seconds}}`

`= \frac{4\ \text{miles}}{120\ \text{seconds}}`

`= \frac{4\ \text{miles}}{120\ \text{seconds}}/\bigg((120)/(120)\bigg)`

`=\frac{0.33\ \text{miles}}{1\ \text{second}}`

*************************************************************************************

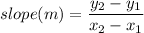
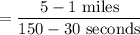
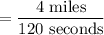
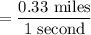
11. Answer: $10 per week

Explanation:

Determine the coordinates in like units where x is weeks and y is total dollars, use the slope formula to find the rate of change, then reduce so the denominator is equal to 1.

(4 weeks, $350) and (9 weeks, $400)

`slope (m) = (y_2-y_1)/(x_2-x_1)`

`= \frac{400-350\ \text{dollars}}{9-4\ \text{weeks}}`

`= \frac{50\ \text{dollars}}{5\ \text{weeks}}`

`= \frac{10\ \text{dollars}}{1\ \text{week}}`

*************************************************************************************

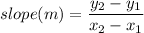
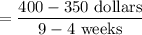
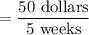
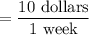
12. Answer: 300 miles per hour

Explanation:

Determine the coordinates in like units where x is hours and y is miles, use the slope formula to find the rate of change, then reduce so the denominator is equal to 1.

(8:00 am, 0 miles) and (1:00 pm, 1500 miles)

= (8 hours, 0 miles) and (13 hours, 1500 miles)

`slope (m) = (y_2-y_1)/(x_2-x_1)`

`= \frac{1500-0\ \text{miles}}{13-8\ \text{hours}}`

`= \frac{1500\ \text{miles}}{5\ \text{hours}}`

`= \frac{300\ \text{miles}}{1\ \text{hour}}`