Answer:
A. Solution to
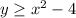 but not to
but not to
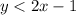
Explanation:
Given
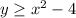
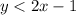
Required
Is
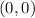 a solution?
a solution?
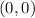 implies that:
implies that:
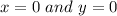
To check if it is a solution or not, we simply substitute 0 for x and for y in the given inequalities
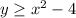 becomes
becomes


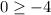
This solution is true
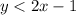 becomes
becomes



This solution is not true because 0 is greater than 1.
Hence, option (A) is correct