Question

Two charges +3μC+3μC and +12μC+12μC are fixed 1 m apart, with the second one to the right. Find the magnitude and direction of the net force on a −2-nC charge when placed at the following locations: (a) halfway between the two (b) half a meter to the left of the +3μC+3μC charge (c) half a meter above the +12μC+12μC charge in a direction perpendicular to the line joining the two fixed charges

Answer 1

a) F_total = -648 10⁻⁴ N

, b) F_total = - 312 N, c) F_total = (38.6 i ^ + 883.4 j ^) 10⁻⁴ N

Step-by-step explanation:

To solve this exercise we will use Coulomb's law

F = k q₁ q₂ / r²

and that forces are vectors

They indicate that the charge q₁ = 3 10⁻⁴ C and the charge q₂ = 12 10⁻⁴ C being separated d = 1 m

Let's place the reference system on the charge q₁

a) we place a third charge q₃ = 2 10⁻⁹ C at the midpoint

r = d / 2

r = ½ m

Since all charges have the same sign, the forces are repulsive, so the total force is

F_total = F₁₃ - F₂₃

let's develop this expression

F_total = k q₁ q₃ / r² - k q₂ q₃ / r²

F_total =
`k (q_(3) )/(r^(2) ) ( q_(1) - q_(2) )`

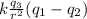
let's calculate

F_total = 9 10⁹ (3- 12) 10⁻⁴

F_total = -648 10⁻⁴ N

b) place the charge q₃ at a distance r = -0.5 m to the left of the charge q₁

F_total = -F₁₃ -F₂₃

F_total = -k q₁ q₃/ r₁₃² - k q₂ q₃ / r₂₃²

F_total = -
`k q_(3) ( (q_(1) )/(r_(13)^(2)) + (q_(2) )/(r_(23)^(2) ) )`

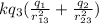
the distances

r₁₃ = 0.5 m

r₂₃ = 0.5 +1 = 1.5 m

calculate

F_total = - 9 10⁹ 2 10⁻⁹ (3 /0.5² + 12 /1.5²) 10⁻⁴

F_total = - 18 (12 + 5.33) 10⁻⁴

F_total = - 312 N

c) the charged q₃ is placed on the charge q₂ on the y axis.

In this case the charge q₂ exerts a force on the y-axis on the charge q₃

F₂₃ = k q₂ q₃ / r² j ^

where r = 0.5 m

let's calculate

F₂₃ = 9 10⁹ 12 10⁻⁴ 2 10⁻⁹ / 0.5²

F₂₃ = 864 10⁻⁴ j ^

Charge q1 exerts a repulsive force on the axis that joins them

F₁₃ = k q₁ q₃ / r₁₃²

let's look for the distance

r₁₃ =

r₁₃ = 1,118 m

Let's use trigonometry to find the direction of this distance

tan θ = y / x

θ = tan⁻¹ (y / x)

θ = tan⁻¹ (0.5 / 1)

θ = 26.6º

let's write this force in its components

F₁₃ = k q₁

(cos 26.6 i ^ + sin 26.6 j ^)

let's calculate

F₁₃ = 9 10⁹ 3 10⁻⁴

(cos 26.6 i ^ + sin 26.6 j ^)

F₁₃ = 43.2 (0.894 i ^ + 0.448 j ^) 10⁻⁴

F₁₃ = (38.6 i ^ + 19.4 j⁾ 10⁻⁴ N

Let's write the total force

F_total = F₁₃ i ^ +

j ^ + F₂₃ j ^

let's substitute

F_total = 38.6 10⁻⁴ i ^ + (19.4 + 864) 10⁻⁴ j ^

F_total = (38.6 i ^ + 883.4 j ^) 10⁻⁴ N