How many lines are determined by the points a b c d and e if 3 of them arent collinear

Question

asked Jul 10, 2021 85.3k views

1 Answer

Benjy Wiener · Answer 1 · 2021-07-14T14:03:17+0000

Answer:

10 possible lines

Explanation:

Given

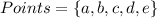
$Points = \{a,b,c,d,e\}$

Required

Number of lines

From the question, the number of points (n) are:

n = 5

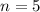
If 3 points are not collinear (i.e. on a straight line), it means that only (5 - 3) of the points can be chosen

So, we have:

n = 5

r = 5 - 3

r =2

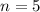
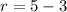
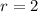
The number of lines is then calculated using combination formula.

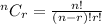
^nC_r = (n!)/((n-r)!r!)

We used combination because the analysis done above implies that 2 points are to be selected from a,b,c,d and e.

To select means combination

Having said that;

Substitute
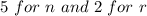
$5\ for\ n\ and\ 2\ for\ r$

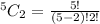
^5C_2 = (5!)/((5-2)!2!)

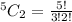
^5C_2 = (5!)/(3!2!)

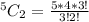
^5C_2 = (5*4*3!)/(3!2!)

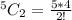
^5C_2 = (5*4)/(2!)

^5C_2 = (5*4)/(2*1)

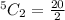
^5C_2 = (20)/(2)

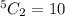
^5C_2 = 10

Hence, there are 10 possible lines