Question

All the edges of a cube are expanding at a rate of 4 in. per second. How fast is the volume changing when each edge is 10 in. long

Answer 1

Given:

All the edges of a cube are expanding at a rate of 4 in. per second.

To find:

The rate of change in volume when each edge is 10 in. long.

Solution:

Let a be the edge of the cube.

According to the question, we get

`(da)/(dt)=4\text{ in./sec}`

`a=10\text{ in.}`

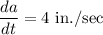
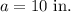
We know that, volume of a cube is

`V=a^3`

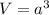
Differentiate with respect to t.

`(dV)/(dt)=(d)/(dt)a^3`

`(dV)/(dt)=(3a^2)* (da)/(dt)`

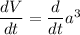
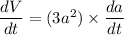
Putting the given values, we get

`(dV)/(dt)=(3(10)^2)* 4`

`(dV)/(dt)=3(100)* 4`

`(dV)/(dt)=300* 4`

`(dV)/(dt)=1200\text{ in}^3\text{/sec}`

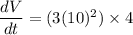
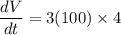
Therefore, the rate of change in volume 1200 cubic inches per second.