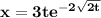Answer:
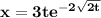
Step-by-step explanation:
From the given information concerning the spring-mass system:
Let us apply Hooke law.
Then, we have:
mg = ks
8 = k4
k = 8/4
k = 2
Provided that the mass weighing 8 lbs is attached to a spring.
Then, we can divide it by gravity 32 ft/s².
∴
m = 8/32
m = 1/4 slugs
The medium that offers the damping force
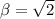
Now, let us set up a differential equation that explains the motion of the spring-mass system.
The general equation is:
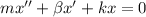
where;
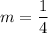
k = 2, and
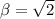
Then;

By solving the above equation, the auxiliary equation is:
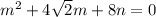
Using quadratic formula:
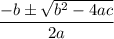
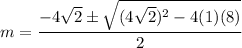
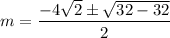

Since this is a repeated root, the solution to their differential equation took the form.
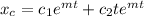
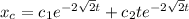
From the initial condition.
At equilibrium position where the mass is being from:
x(0) = 0
Also, at the downward velocity of 3 ft/s
x'(0) = 3
Then, at the first initial condition:
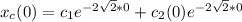


At the second initial condition;
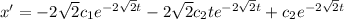
where;
x'(0) = 3
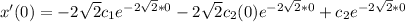
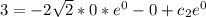


Replacing in the constraints, the equation of the motion is: